
Calculs vient du latin « Calculus » : caillou
La légende raconte que les bergers déposaient dans un panier autant de cailloux que de moutons quittaient la bergerie. En rentrant des prés, le berger sortait les cailloux du panier afin de vérifier le compte de moutons.
Les symboles « + » et « – » sont introduits par l’allemand Johannes Widdmann en 1489 pour les besoins du commerce.
Le symbole « + » serait un symbole « – » barré.
Le mot « somme » vient du latin « summa » signifiant « le point le plus élevé ».
Le symbole « x » vient de l’anglais William Oughtred en 1631.
Le symbole « = » introduit par l’anglais Robert Recorde en 1557 qui le voyait comme deux lignes jumelles.
Rien est pareil que de jumeaux (Recorde)
Partie 1 : Méthode de Calcul mental
Méthode 1 : Effectuer des additions et soustractions avec les nombres décimaux1
Méthode 2 : Additionner ou soustraire par 9, 99, 0.9, 101, 1001 …2
Méthode 3 : Multiplier par 10, 100, 1 0003
Méthode 4 : Diviser par 10, 100, 1 0004
Méthode 5 : Multiplier par 0.15
Méthode 6 : Multiplier par 0,56
Méthode 7 : Multiplier par 47
Méthode 8 : Diviser par 48
Méthode 9 : Multiplier par 59
Méthode 10 : Diviser par 510
Méthode 11 : Diviser avec les tables de multiplication
Partie 2 : Calculer astucieusement
Méthode 12 : Regrouper astucieusement les termes11
Méthode 13 : Regrouper astucieusement les facteurs12
Partie 3 : La distributivité
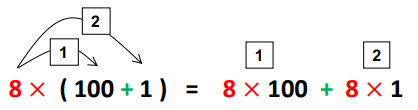
Ainsi : 8 x 101 = 800 + 8 = 808
Méthode 14 : Appliquer la distributivité au calcul mental13
Méthode 15 : Appliquer la distributivité au calcul mental
Partie 4 : Ordre de grandeur
Méthode 16 : Calculer un ordre de grandeur dans un calcul
Annexe : Astuces
- 42,5 + 29,36 n’est pas égal à 71,41 car 36 et 5 n’ont pas le même rang. ↩︎
- A = Ajouter 299, c’est ajouter 300 puis enlever 1
B = Enlever 0.9, c’est enlever 1 puis ajouter 0.1
C = Ajouter 101, c’est ajouter 100 puis ajouter 1 ↩︎ - Multiplier par 1000 (3 zéros), c’est « grandir » de 3 rangs ↩︎
- Diviser par 100 (2 zéros), c’est « réduire » de 2 rangs ↩︎
- Multiplier par 0.1, c’est diviser par 10 ↩︎
- Multiplier par 0.5, c’est diviser par 2 ↩︎
- Multiplier par 4, c’est multiplier par 2 puis multiplier par 2 ; ↩︎
- Diviser par 4, c’est diviser par 2 puis diviser par 2 ↩︎
- Multiplier par 5, c’est multiplier par 10 puis diviser par 2 ↩︎
- Diviser par 5, c’est diviser par 10 puis multiplier par 2 ↩︎
- Pour le calcul d’une somme, l’ordre des termes n’a pas d’importance ↩︎
- Pour le calcul d’un produit, l’ordre des facteurs n’a pas d’importance. ↩︎
- On connaît des règles de calcul mental pour multiplier par 10, par 100, par
1 000, par 2, etc… On décompose donc un des facteurs en somme ou différence formée de termes du type 10, 100, 1, 2, etc… ↩︎
Leave a Reply